|
r
. Соответствующие векторы на фазовой диаграмме будут повернуты по отношению друг к другу на угол |
 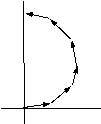
j
=
p
D
j
|
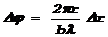 . .
При достаточно большом радиусе будет
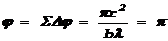 . .
Соответствующий радиус r1
называется (внешним) радиусом первой зоны Френеля. При дальнейшем увеличении радиуса, естественно, величина j
будет увеличиваться. Из условия j
=
k
p
мы получаем выражение для радиуса k
-й зоны Френеля:
 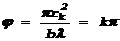 ; ;  . .
|
 E0 E0
|
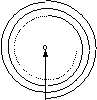
Мы уже достаточно много работали с векторными диаграммами, и должно быть понятно, что при дальнейшем увеличении радиуса отверстия (по сравнению с r1
) амплитуда суммарных колебаний в точке наблюдения, пропорциональная длине отрезка (вектора), соединяющего начало и конец дуги, будет уменьшаться. Она достигнет минимума, когда радиус отверстия достигнет внешнего радиуса второй зоны Френеля. Но в отличии от задачи о колебаниях волны, излучаемой щелью при дифракции Фраунгофера, дуга не замкнется в окружность, мы получим некоторую скручивающуюся спираль. Длина вектора, проведенного от начала к центру спирали, дает, очевидно, амплитуду падающей волны - скручивание спирали к центру соответствует бесконечно большому радиуса отверстия, когда дифракция не наблюдается.
Подобная спираль, которую называют спиралью Френеля, получается и в том случае, когда на отверстие падает сферическая волна конечного радиуса a
.
Выражение для радиусов зон Френеля в этом случае, естественно, иное.
На рисунке a
- радиус фронта волны, b
- расстояние от фронта до точки наблюдения P
. Таким образом, расстояние от источника света S
до точки наблюдения вдоль оси равно (a+b)
.
Подсчитаем теперь длину некоторого произвольного луча. Как и раньше, рассматриваем лишь параксиальные лучи. При таком ограничении наши выражения будут приближенными.
Нижний катет прямоугольного треугольника, образованного радиусом фронта a
, осью системы и радиусом rнекоторого кольца на фронте волны, будет равен
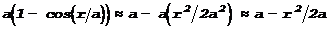 . .
Расстояние от источника света до края кольца и от него до точки наблюдения будет равен
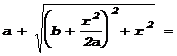
Перейти на страницу: 1 2 3 |