|
Важнейшей характеристикой линейной распределенной системы является закон дисперсии, который связывает волновое число и частоту монохроматической волны. Он может быть записан как  , ,  или в неявной форме или в неявной форме 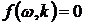 . .
Когда плоская волна описывается одним (вообще говоря, интегродифференциальным) уравнением, закон дисперсии получают, отыскивая его решение в виде 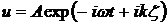 . В простейшем случае процесс распространения волны описывается уравнением . В простейшем случае процесс распространения волны описывается уравнением
 . .
При этом волновое число связано с частотой линейной зависимостью 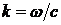 , или , или  , где скорость распространения волны , где скорость распространения волны 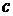 есть постоянная величина. Однако уже при учете диссипативных процессов поведение волны описывается более сложными уравнениями. Закон дисперсии есть постоянная величина. Однако уже при учете диссипативных процессов поведение волны описывается более сложными уравнениями. Закон дисперсии  также усложняется. Для звуковых волн в вязкой теплопроводящей среде и электромагнитных волн в среде с проводимостью справедливы следующие соотношения между волновым числом и частотой: также усложняется. Для звуковых волн в вязкой теплопроводящей среде и электромагнитных волн в среде с проводимостью справедливы следующие соотношения между волновым числом и частотой:
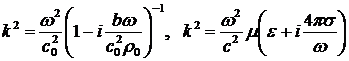 . .
В более общих случаях от частоты могут сложным образом зависеть действительная и мнимая части волнового числа:
 . .
Действительная часть характеризует зависимость от частоты фазовой скорости распространения волны 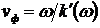 , а мнимая часть — зависимость коэффициента затухания волны от частоты. , а мнимая часть — зависимость коэффициента затухания волны от частоты.
Во многих случаях волновой процесс удобно описывать не одним уравнением типа волнового, а системой связанных интегродифференциальных уравнений  . Здесь . Здесь 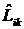 — матричный оператор, действующий на вектор-столбец — матричный оператор, действующий на вектор-столбец  .В качестве .В качестве  , например, для акустических волн может служить совокупность переменных , например, для акустических волн может служить совокупность переменных 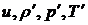 (колебательная скорость, приращения плотности, давления, температуры), а для электромагнитных волн — компоненты векторов напряженностей электрического и магнитного полей, электрического смещения и магнитной индукции. В этом случае формальная схема отыскания закона дисперсии такова. Ищем решение системы в виде (колебательная скорость, приращения плотности, давления, температуры), а для электромагнитных волн — компоненты векторов напряженностей электрического и магнитного полей, электрического смещения и магнитной индукции. В этом случае формальная схема отыскания закона дисперсии такова. Ищем решение системы в виде 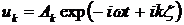 : :
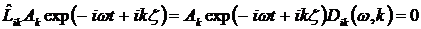 , ,
Решение будет нетривиальным, только если 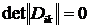 . Отсюда получаются искомые зависимости . Отсюда получаются искомые зависимости 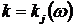 . Наличие у дисперсионного уравнения нескольких корней . Наличие у дисперсионного уравнения нескольких корней 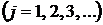 означает, что система может описывать несколько типов собственных волн (мод) среды. означает, что система может описывать несколько типов собственных волн (мод) среды.
Частотная дисперсия приводит к изменению закономерностей распространения немонохроматических волн. Действительно, различные спектральные компоненты обладают в диспергирующей среде отличающимися скоростями и коэффициентами затухания:
 . .
В силу дисперсии фазовой скорости в процессе распространения изменяются фазовые соотношения между спектральными компонентами. Следовательно, изменяется результат их интерференции: форма немонохроматической волны искажается. Дисперсия коэффициента поглощения  приводит к трансформации частотного спектра волны приводит к трансформации частотного спектра волны 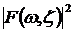 и дополнительному искажению формы импульса. и дополнительному искажению формы импульса.
|