Рассмотренный метод вывода кинетического уравнения Больцмана вполне удовлетворителен с физической точки зрения. Однако кинетическое уравнение может быть так же получено из математического аппарата, применяемого для описания движения частиц газа. В 1946 году такой вывод, получивший название динамического, бал дан Н. Н. Боголюбовым. Метод Боголюбова позволяет не только получить уравнение Больцмана, но и поправки к нему, т.е. члены следующих порядков по малому параметру газовости . Например, в указанном выводе учитывается одновременное столкновение только двух молекул и предполагается, что столкновения происходят в одной точке, т.е. являются локальными, и нет более или менее очевидного рецепта, позволяющего учесть столкновения групп из трёх, четырёх и большего числа частиц. Между тем ясно, что учёт подобных столкновений принципиально важен при рассмотрении плотных газов. В связи с этим целесообразно более строго подойти к выводу кинетического уравнения и к его возможным обобщениям. Метод Боголюбова позволяет учесть

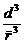“нелокальность” столкновения и столкновения более, чем двух частиц при помощи определённых поправочных членов, возникающих при выводе. Пренебрежение поправками приводит кинетическое уравнение к виду, полученному в простейшем случае.

Список литературы.

1. Е.М.Лифшиц, Л.П.Питаевский. Физическая кинетика. Наука, М., 1979 г.

2. Ю.Б.Румер, М.Ш.Рывкин. Термодинамика, статистическая физика и кинетика.

Наука, М., 1972 г.