|
Дисперсионные эффекты часто проявляются при распространении электромагнитных волн. Покажем, как видоизменяются исходные уравнения при учете этих свойств. Система уравнений Максвелла сохраняет свой вид. Свойства среды должны быть учтены в материальных уравнениях:
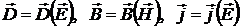 . .
Для статических и медленно изменяющихся полей можно написать
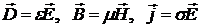 , ,
где 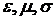 — константы, т. е. значения — константы, т. е. значения 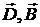 и и 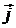 в некоторой точке среды и в некоторый момент времени определяются значениями в некоторой точке среды и в некоторый момент времени определяются значениями 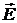 и и 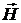 в той же точке и в тот же момент времени. в той же точке и в тот же момент времени.
При быстром изменении поля вследствие инерции внутренних движений и наличия пространственной микроструктуры среды наблюдается зависимость поляризации от поля, действующего в других точках и в другие моменты времени. При этом нужно иметь в виду, что в силу условия причинности поляризация и, следовательно, индукция зависят от полей, действовавших только в предыдущие моменты времени.
Сказанное можно записать математически, представляя материальные уравнения в общей интегральной форме:
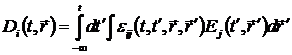 , (1.1) , (1.1)
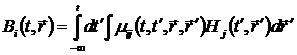 , (1.2) , (1.2)
 . (1.3) . (1.3)
По дважды встречающимся индексам здесь и везде в дальнейшем предполагается суммирование.
Выражения (1.1) — (1.3) представляют собой наиболее общую функциональную форму записи материальных уравнений для линейной среды. В этой записи учтена возможность проявления нелокальности, запаздывания и анизотропных свойств среды.
В частном случае, если среда однородна в пространстве и не изменяет со временем своих свойств, материальные характеристики  , ,  , , 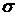 должны зависеть лишь от разностей координат должны зависеть лишь от разностей координат  и времени и времени  . Тогда . Тогда
 , (1.4) , (1.4)
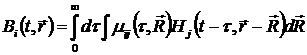 , (1.5) , (1.5)
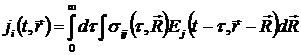 . (1.6) . (1.6)
Связь между электрическим смещением и магнитной индукцией, полями и поляризациями среды определяется соотношениями
 . (1.7) . (1.7)
Поэтому материальные уравнения можно записать также в виде
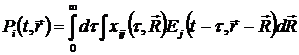 , (1.8) , (1.8)
где 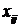 — тензор восприимчивости среды. Аналогичное выражение можно записать для — тензор восприимчивости среды. Аналогичное выражение можно записать для 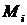 . .
Для проведения дальнейшего анализа удобно разложить 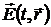 по плоским волнам: по плоским волнам:
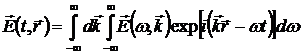 . .
После обычного перехода в фурье-представление в выражениях для 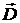 и и 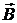 получаем простую зависимость получаем простую зависимость
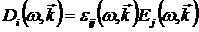 , (1.9) , (1.9)
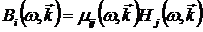 , (1.9) , (1.9)
где
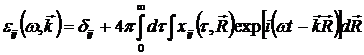 . (1.10) . (1.10)
Видно, что компоненты тензора диэлектрической проницаемости зависят в общем случае от частоты и от волнового вектора волны.
Аналогичный вывод можно сделать для магнитной проницаемости 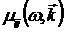 и проводимости и проводимости  . .
Таким образом, дисперсия при распространении электромагнитных волн может проявляться двояким образом — как частотная (за счет зависимости  , ,  , , 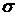 от частоты) и как пространственная (за счет зависимости этих же параметров от волнового вектора от частоты) и как пространственная (за счет зависимости этих же параметров от волнового вектора 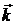 ). Частотная дисперсия существенна, если частота электромагнитных волн близка к собственным частотам колебаний в среде. Пространственная же дисперсия становится заметной, когда длина волны сравнима с некоторыми характерными размерами. ). Частотная дисперсия существенна, если частота электромагнитных волн близка к собственным частотам колебаний в среде. Пространственная же дисперсия становится заметной, когда длина волны сравнима с некоторыми характерными размерами.
Перейти на страницу: 1 2 3 |