|
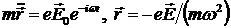 . .
Здесь  — масса и заряд электрона. Мы не учитываем силу, действующую на заряд со стороны магнитного поля, так как рассматривается нерелятивистский случай ( — масса и заряд электрона. Мы не учитываем силу, действующую на заряд со стороны магнитного поля, так как рассматривается нерелятивистский случай (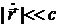 ). Поляризация среды (дипольный момент единицы объема, содержащей ). Поляризация среды (дипольный момент единицы объема, содержащей 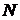 электронов) равна электронов) равна
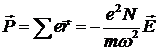 . .
Отсюда 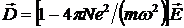 и и
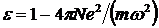 . (1.17) . (1.17)
При  мы получаем из (1.17) прежний результат: мы получаем из (1.17) прежний результат: 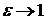 и и 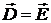 . Область применимости формулы (1.17) для сред, в которых нет свободных электронов, лежит в диапазоне далекой ультрафиолетовой области для самых легких элементов. . Область применимости формулы (1.17) для сред, в которых нет свободных электронов, лежит в диапазоне далекой ультрафиолетовой области для самых легких элементов.
С учетом (1.16) уравнения Максвелла для комплексных амплитуд примут вид
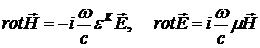 , (1.18) , (1.18)
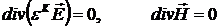 . (1.18) . (1.18)
Поясним вывод уравнения 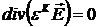 . Из уравнения непрерывности при гармонической зависимости от времени следует, что . Из уравнения непрерывности при гармонической зависимости от времени следует, что
 . .
Подставляя это соотношение в уравнение Максвелла  , запишем его в форме , запишем его в форме
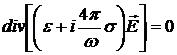 . .
Учитывая определение 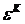 , получим уравнение , получим уравнение 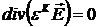 . .
Таким образом, для высокочастотных монохроматических полей вместо диэлектрической проницаемости и проводимости удобно ввести комплексную диэлектрическую проницаемость, объединяющую оба эти понятия. Физически это означает, что ток в среде для высокочастотных полей нецелесообразно рассматривать как сумму тока проводимости и тока смещения. Вместо этого вводится полный ток
 , (1.19) , (1.19)
где 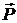 — комплексный вектор поляризации среды. — комплексный вектор поляризации среды.
Перейти на страницу: 1 2 3 |